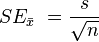What is the difference between the sample average, Ȳ, and the population mean?
The sample average is the average of the samples taken from a population. The population mean is the average of the entire population. They are guaranteed to be the same if and only if the sample includes the entire population.
What is the difference between the estimator and the estimate?
The estimator is a function of the sample data. The sample data is drawn randomly from the population. The estimator is a function that is used to make an educated guess of one of the parameters in the population such as the population mean. And example of the estimator is a function that produces Ȳ where Ȳ is the sample mean. For example, if n samples are taken from a population of 10 things, Ȳ = (1/n) * sum(X1 + X2 + X3 + X4) where X1, X2, X3, and X4, are the sample values. The population mean itself = (1/10) * sum(X1 + X2 + X3 + X4 + X5 + X6 + X7 + X8 + X9 + X10).
In this case, the estimator is the function (1/n) * sum(X1 + X2 + X3 + x4).
Assume that a population distribution has a mean of 10 and a variance of 16. Determine the mean and variance of Ȳ from an i.i.d. sample from this population for n = 10.
The mean of the population sample is expected to be 10. The variance of Ȳ is expected to be = (Population Variance / n) = 16/10 = 1.6. Obviously, as we take more and more samples from the population, the variance of the sample mean will converge toward zero. For example, if we take 1000 samples, the variance of Ȳ , the sample mean, will be 0.016. By this point, we can be reasonably sure that the sample mean is very close to 10.
The fact that the sample variance approaches 0 with large numbers of samples (n) and that the sample mean approaches the population mean is a result of the Law of Large Numbers.
What role does the central limit theorem play in hypothesis testing in statistics? What role does it play in the construction of confidence intervals?
Due to the Central Limit Theorem, the distributions of sample means for multiple samples of a population is, itself, a distribution. The distribution of the sample means is approximates a Normal Distribution if there are enough samples. Because of this, confidence intervals can be constructed using standard deviations around the sample mean. For example, (±1.96 * (Sample Mean Standard Deviation)) gives us a 95% certainty that the population mean falls within a set of values.
How many samples are “enough?” Well, it depends on how the population values are distributed. But, usually 30 samples are enough to construct a reasonable approximation to the Normal Distribution.
What is the difference between a null hypothesis and an alternative hypothesis?
A null hypothesis is a value that is chosen and assumed to be true. The alternate hypothesis is a value that is chosen and assumed to be true if the null hypothesis is false.
What is the “size of a test?”
The size of a test is the probability that a test rejects the null hypothesis even though the null hypothesis is really true.
What is the significance level?
A person chooses a significance level for a test (e.g., 50%, 75%, 90%, 95%, or 99%) and uses it as a criteria to reject a hypothesis test if the null hypothesis is true.
What is the definition of “power?”
The power is the probability that a test rejects the null hypothesis when the alternative hypothesis is true.
What is the difference between a one sided and a two sided alternative hypothesis?
With a one sided hypothesis, the value of interest is only on one side (> or <) the null hypothesis. Under the two sided alternate hypothesis, the value of interest is not equal to the null hypothesis value.
Why does a confidence interval contain more information than the result of a single hypothesis test?
The confidence interval contains all values that reject the null hypothesis. Since the sample mean is normally distributed, then the confidence interval contains values that are at least a given amount larger than the sample mean as well as values that are at least a given amount smaller than the sample mean.
Why is the differences-of-means estimator, applied to data from a randomized controlled experiment, an estimator of the treatment effect?
The “treatment effect” is the causal effect in an experiment or quasi-experiment. The causal effect is the expected effect of a given treatment or intervention in an ideal randomized controlled experiment. An example of a “treatment effect” is the expected result of giving a drug to a population versus not giving it to an identical population. Another example is the expected result of giving fertilizer to plants versus not giving it to other plants growing in otherwise identical conditions.
The differences-in-mean estimator is the differences in mean between the control groups (those that have not received the treatment) and the treatment groups. Remember, for such experiments to have any meaning, the control group and treatment group must be randomly selected from the sample (identical) population.